MEDIA Y VARIANZA DE VARIABLES ALEATORIAS CONTINUAS
Bernoulli
Es un experimento estadístico en el que pueden haber únicamente dos resultados posibles. Es costumbre designarlos como “éxito” y “fracaso” aunque pueden tener otra representación y estar asociados a algún otro significado de interés.
Si la probabilidad de obtener “éxito” en cada ensayo es un valor que lo representamos con p, entonces, la probabilidad de obtener “fracaso” será el complemento q = 1 – p.
Binomial:
Esta distribución es muy importante y de uso frecuente. Corresponde a experimentos con características similares a un experimento de Bernoulli, pero ahora es de interés la variable aleatoria relacionada con la cantidad de “éxitos” que se obtienen en el experimento.
Características de un Experimento Binomial
a) La cantidad de ensayos n, que se realizan es finita.
b) Cada ensayo tiene únicamente dos resultados posibles: “éxito” o “fracaso”
c) Todos los ensayos realizados son independientes
d) La probabilidad p, de obtener “éxito” en cada ensayo permanece constante.
En el siguiente video podemos ver claramente la distribución binomial:
CLASE 5: 6/01/2017
En esta clase realizamos varios ejercios de los temas antes mensionados, a continuación podemos ver un ejemplo muy claro:
CLASE 6: 11/01/2017
DISTRIBUCIÓN HIPERGEOMÉTRICA
Esta distribución se refiere a los experimentos estadísticos que consisten en tomar una muestra sin reemplazo, de un conjunto finito el cual contiene algunos elementos considerados “éxitos” y los restantes son considerados “fracasos”.
Tomar una muestra sin reemplazo significa que los elementos son tomados uno a uno, sin devolverlos. Podemos concluir entonces que los ensayos ya no pueden ser considerados independientes porque la probabilidad de “éxito” al tomar cada nuevo elemento es afectada por el resultado de los ensayos anteriores debido a que la cantidad de elementos de la población está cambiando.
MEDIA Y VARIANZA
DISTRIBUCIÓN GEOMÉTRICA
Es un caso especial de la distribución binomial negativa, cuando k=1. Es decir interesa conocer la probabilidad respecto a la cantidad de ensayos que se realizan hasta obtener el primer “éxito”
MEDIA Y VARIANZA
CLASE 7: 13/01/2017
DISTRIBUCIÓN HIPERGEOMÉTRICA:
La distribución hipergeométrica es una distribución discreta que modela el número de eventos en una muestra de tamaño fijo cuando usted conoce el número total de elementos en la población de la cual proviene la muestra. Cada elemento de la muestra tiene dos resultados posibles (o es un evento o un no evento). Las muestras no tienen reemplazo, por lo que cada elemento de la muestra es diferente. Cuando se elige un elemento de la población, no se puede volver a elegir. Por lo tanto, la probabilidad de que un elemento en particular sea seleccionado aumenta con cada ensayo, suponiendo que aún no ha sido seleccionado.

DISTRIBUCIÓN BINOMIAL NEGATIVA:

DISTRIBUCIÓN HIPERGEOMÉTRICA:
La distribución hipergeométrica es una distribución discreta que modela el número de eventos en una muestra de tamaño fijo cuando usted conoce el número total de elementos en la población de la cual proviene la muestra. Cada elemento de la muestra tiene dos resultados posibles (o es un evento o un no evento). Las muestras no tienen reemplazo, por lo que cada elemento de la muestra es diferente. Cuando se elige un elemento de la población, no se puede volver a elegir. Por lo tanto, la probabilidad de que un elemento en particular sea seleccionado aumenta con cada ensayo, suponiendo que aún no ha sido seleccionado.

MEDIA Y VARIANZA:
DISTRIBUCIÓN BINOMIAL NEGATIVA:
MEDIA Y VARIANZA:

DISTRIBUCIÓN GEOMÉTRICA:


MEDIA Y VARIANZA:

CLASE 8: 18/01/2017
DISTRIBUCIONES DE PROBABILIDADES EN VARIABLES CONTINUAS


DISTRIBUCIÓN GEOMÉTRICA:
MEDIA Y VARIANZA:

CLASE 8: 18/01/2017
DISTRIBUCIONES DE PROBABILIDADES EN VARIABLES CONTINUAS
Una distribución continua describe las probabilidades de los posibles valores de una variable aleatoria continua. Una variable aleatoria continua es una variable aleatoria con un conjunto de valores posibles (conocido como el rango o respaldo) que es infinito y no se puede contar.
Las probabilidades de variables aleatorias continuas (X) se definen como el área por debajo de la curva de la distribución. Por lo tanto, solo los rangos de valores pueden tener una probabilidad diferente de cero. La probabilidad de que una variable aleatoria continua equivalga a algún valor siempre es cero.

FUNCIÓN DE DISTRIBUCIÓN DE PROBABILIDAD

DISTRIBUCIÓN NORMAL
La distribución normal fue estudiada por Gauss. Se trata de una variable aleatoria continua (la variable puede tomar cualquier valor real). La función de densidad tiene forma de campana. Dos parámetros determinan una distribución normal: la media y la desviación típica.


La distribución normal estándar, o tipificada o reducida, es aquella que tiene por media el valor cero, μ = 0, y por desviación típica la unidad, σ =1.

Esta tabla nos ayuda a encontrar los valores que dificilmente podemos encontrarlos manualmente.

DISTRIBUCIÓN NORMAL
La distribución normal fue estudiada por Gauss. Se trata de una variable aleatoria continua (la variable puede tomar cualquier valor real). La función de densidad tiene forma de campana. Dos parámetros determinan una distribución normal: la media y la desviación típica.

La gráfica de f es similar al perfil del corte vertical de una campana y tiene las siguientes características:
1) Es simétrica alrededor de μ
2) Su asíntota es el eje horizontal
3) Sus puntos de inflexión están ubicados en μ – σ y μ + σ
DISTRIBUCIÓN NORMAL ESTÁNDAR
La distribución normal estándar, o tipificada o reducida, es aquella que tiene por media el valor cero, μ = 0, y por desviación típica la unidad, σ =1.
Esta tabla nos ayuda a encontrar los valores que dificilmente podemos encontrarlos manualmente.
CLASE 9: 20/01/2017
EVALUACIÓN DEL SEGUNDO BIMESTRE
CLASE 10: 25/01/2017
ESTANDARIZACIÓN DE LA DISTRIBUCIÓN NORMAL
Todas las distribuciones normales N(µ, σ), pueden ponerse mediante una traslación µ, y un cambio de escala σ, como N(0,1). Esta distribución especial se llama normal estandarizada o tipificada.

CLASE 11: 27/01/2017
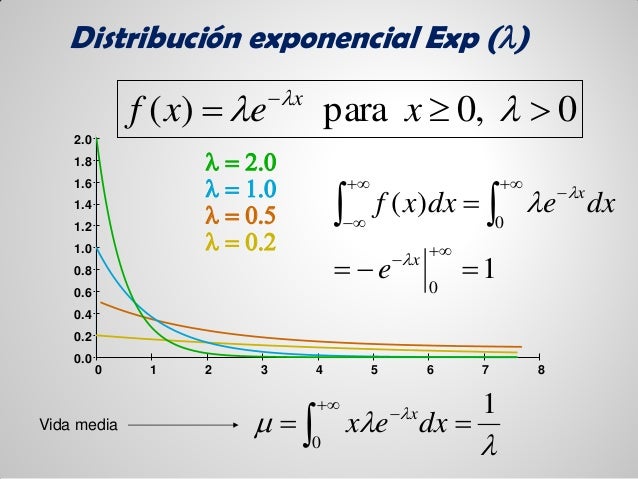
DISTRIBUCIÓN EXPONENCIAL

Utilice la distribución exponencial para modelar procesos de Poisson, en los cuales los eventos ocurren de manera continua e independiente a una tasa constante.
Esta distribución tiene una amplia gama de aplicaciones, que incluyen el análisis de fiabilidad de productos y sistemas, teorías de colas y cadenas de Markov.
Por ejemplo, la distribución exponencial se puede utilizar para modelar:
- Cuánto tiempo tarda un componente electrónico en fallar
- El intervalo de tiempo entre las llegadas de clientes a un terminal
- El tiempo que esperan los clientes en fila hasta recibir servicio
- El tiempo hasta que se declara el incumplimiento de un pago (modelos de riesgo de crédito).

No hay comentarios:
Publicar un comentario